[프로그래머스-Lv2-JAVA] 요격 시스템
이 문제 풀이는 [프로그래머스-Lv1-JAVA] 신고 결과 받기에서 LEVEL 2로의 스텝업 필요성을 느껴 LEVEL2 카테고리에 처음으로 진입한 문제 풀이에 해당한다.
1. 문제
문제 캡처
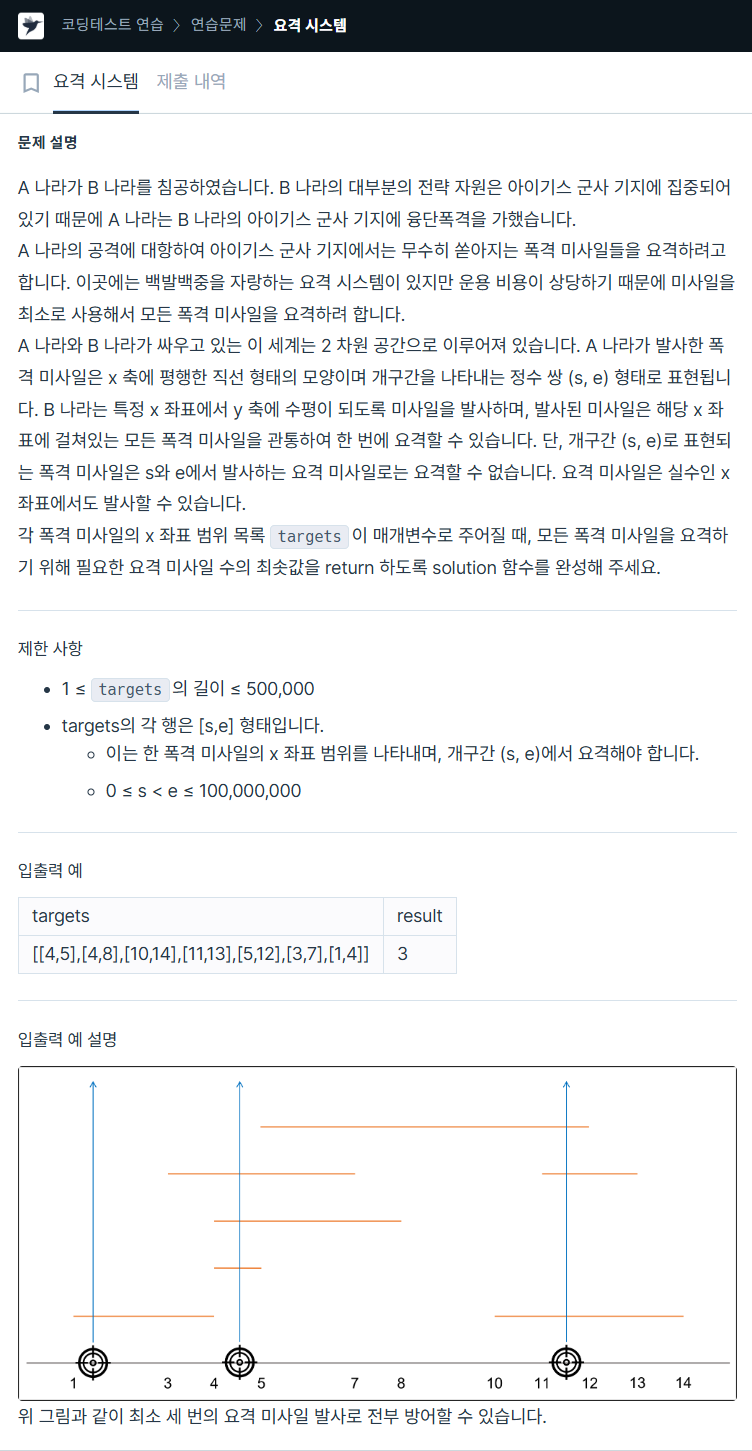
이 문제는 x 좌표의 범위로 표현되는 폭격 미사일 요격 범위들이 주어지고 x 좌표에서 발사되어 x 좌표가 포함된 폭격 미사일을 모두 요격할 수 있는 요격 미사일을 발사할 수 있다. 모든 폭격 미사일을 격추시키기 위한 최소한의 요격 미사일 발사 개수를 구하는 문제이다.
2. 문제 분석
문제를 보면 1차원 x좌표 상에서 주어진 모든 구간을 커버하는 최소 개수의 발사 위치(이하 기준점)를 구하는 문제이다. 이를 해결하기 위한 핵심 논리를 다음과 같이 작성해 보았다.
- 구간 집합의 정의
어떤 구간 [a, b]를 커버하기 위해서는 기준점이 이 구간 내에 포함되어야 한다. 또한, 동일한 기준점을 공유하는 범위 내의 다른 구간들도 동시에 커버할 수 있다. 이와 같이 기준점 1개에 의해 커버 가능한 구간들의 집합을 구간 집합이라고 하자. - 결정 구간 정의
각 구간 집합 내에는 반드시 커버해야 하는 구간이 존재한다. 그것은 집합 내의 가장 빨리 끝나는 구간이며 만약 기준점이 가장 빨리 끝나는 이 구간을 벗어나면, 해당 구간을 커버하기 위해 새로운 기준점이 필요해진다. 따라서 가장 빠르게 끝나는 이 구간을 집합을 결정하는 구간이라고 해서 이를 결정 구간이라고 하자. - 구간 집합 범위 정의
결정 구간과 구간 집합의 정의를 통해 구간 집합의 범위는 다음과 같이 정의될 수 있다.- 시작점: 결정 구간과 범위를 공유하는 구간 중 가장 빠른 시작점
- 종료점: 결정 구간의 종료점.
- 구간 집합 개수 최소화
구간 집합 개수 최소화는 결국 결정 구간의 판별과 결정 구간 내 기준점 배치 위치가 결정한다. 이를 토대로 프로그램상의 해결 흐름을 아래와 같이 작성해 보았다.
- 모든 구간을 끝나는 기준으로 오름차순으로 정렬한다. 이는 구간 집합의 종료점으로 구간 집합이 분리되기 때문이다. 하지만 아직 최소화된 결정 구간이 확정된 시점은 아니며 이 시점에는 모든 구간이 결정 구간이 된다.
- 종료점 기준 정렬된 모든 구간을 순차적으로 확인
- 맨 처음 구간은 기준점 설정이 반드시 필요하므로 기준점을 구간이 끝나는 지점에 설정한다. 구간 마지막에 기준점을 설정하는 이유는 기준점이 결정 구간 뒤에 위치할수록 뒤에 시작되는 구간들을 더 많이 포함하며 결과적으로 커버 가능한 구간이 넓어지기 때문이다.
- 다음 구간을 확인 시 이전에 설정한 기준점 범위 내에 있는지 확인한다. 범위 내에 있다면 이전 결정 구간의 구간 집합 요소가 되며 결정 구간에서 탈락한다.
- 다음 구간이 기준점을 벗어난다면 새로운 구간 집합이 확정됐으므로 현재 결정 구간에 기준점을 추가한다.
- 모든 구간을 확인할 때까지 반복하여 최소화된 구간 집합을 확정하고 개수를 반환한다.
- 결론
이 문제에서 요구하는 미사일 발사 위치의 최소화는 모든 폭격 가능 구간을 끝나는 구간 기준으로 오름차순 정렬하고 구간들을 확인하며 구간이 끝나는 지점에 기준점을 설정하는 방식으로 집합을 최대 넓이로 확인하며, 구간마다 이전에 끝나는 구간의 기준점이 현재 구간이 포함 가능한지 여부로 구간 집합의 포함 및 분리를 판별, 이를 통해 구간 집합의 개수를 최소화하여 풀이 가능하다. 풀이에 대한 논리와 흐름을 정의하였으니 코드로 구현해 보자.
3. 코드 작성
class Solution {
public int solution(int[][] targets) {
// 주어진 폭격 가능 구간들을 끝나는 지점을 기준으로 오름차순 정렬
// 이 시점에서는 모든 구간이 결정 구간이다.
Arrays.sort(targets, (a, b) -> Integer.compare(a[1], b[1]));
// 구간 집합의 개수
int count = 0;
// 현재 설정된 기준점 위치 변수
// 최초 구간은 기준점 설정이 반드시 필요하므로 가장 작은 값으로 초기값 설정
int lastIntercepted = Integer.MIN_VALUE;
// 정렬된 모든 구간을 확인
for (int[] target : targets) {
// target[0]: 현재 구간의 시작점
// target[1]: 현재 구간의 끝점
// 만약 현재 구간의 시작점이 이전 결정 구간을 벗어났다면 새로운 구간 집합으로 분리
if (target[0] > lastIntercepted) {
// 새로운 구간 집합의 결정 구간 마지막 위치에 기준점 설정
lastIntercepted = target[1] - 1;
// 구간 집합 개수 증가
count++;
}
// 시작점이 이전 집합의 기준점 범위 내라면 해당 집합에 포함되며 별도의 작업이 필요 없다.
}
// 모든 구간 확인 후 최소화된 구간 집합 개수 반환.
return count;
}
}4. 회고
LEVEL1 문제는 일반적인 실무 수준의 요구사항 범위였다면 LEVEL2 인 이 문제부터는 본격적으로 알고리즘 문제를 해결하는 느낌이 들었다. 이전 문제들과 같이 해결 방법이 직관적으로 떠오르지 않고 효율적인 해결을 위해 논리를 구성해야 했으며 논리 구성 과정도 개인적으로 꽤 높은 수준으로 구성해야 명확하게 풀 수 있는 문제였다. 단 하나의 레벨 차이인데 극명하게 난도 차이가 발생하였으며 이제 알고리즘의 세계에 본격적으로 입문한 느낌이 든다.
문제를 해결하고 나서 이 문제에 대한 표준적인 해결 방법을 검색해 보았으며 이 문제는 그리디 알고리즘으로 해결하는 문제라고 한다. 그리디 알고리즘의 개념을 보니 논리 구성을 통한 해결 과정과 거의 일치하는 것으로 보이며 직접 논리 구성을 통해 효율적인 해결 방법을 도출한 결과가 그리디 알고리즘과 개념적으로 거의 유사한 만큼 그리디 알고리즘의 개념만 보아도 어떤 목적과 구조로 문제를 해결하는지 정확하게 이해가 되었다.
이제 막 입문한 단계이기는 하지만 정확한 논리 구성과 해결 과정을 효율적으로 분해한다면 결국 컴퓨터의 연산 구조상 최적의 해결 방법은 쉬운 문제일수록 하나로 수렴하는 게 아닐까 하는 생각이 든다.
이 문제는 논리 구성과 효율적인 풀이 구상까지 4시간 이상으로 꽤 오랜 시간이 걸렸다. 하지만 오래 걸린다고 스트레스를 받지는 않았으며 오히려 퍼즐을 풀 듯이 구상한 논리들이 하나씩 맞아떨어지고 결국 효율적인 해결 방법을 떠올렸을 때 벅찬 감동까지 느꼈다. 이 처럼 나는 문제에 직면했을 때 해결 과정 자체를 즐기는 편이다. 하지만 이 방식은 결과 위주의 최단 목표 달성이라는 관점에서는 효율적인 학습 방법은 아니다. 문제 풀이가 지연되면 정답을 빠르게 확인하며 다음 스텝까지 빠르게 진행하는게 정답이라고 생각하는 사람도 있을 것이며, 이 방법이 틀린 방법은 분명 아니다. 하지만 나 같은 경우 시간적인 제약이 크지 않은 경우 아주 기초부터 혼자 생각하면서 차곡차곡 쌓아가는 느낌으로 학습하는 편이다. 이는 입문부터 특정 목표 달성까지에 걸리는 시간은 분명 남들보다 느리겠지만 개념이 완성되는 후반부에는 분명 내 학습 방법도 강점이 있다고 생각한다.
'알고리즘 풀이 기록 > 프로그래머스' 카테고리의 다른 글
| [프로그래머스-Lv2-JAVA] 아날로그 시계 (2) | 2025.01.14 |
|---|---|
| [프로그래머스-Lv2-JAVA] 광물 캐기 (1) | 2024.12.23 |
| [프로그래머스-Lv1-JAVA] 신고 결과 받기 (0) | 2024.12.03 |
| [프로그래머스-Lv1-JAVA] 성격 유형 검사하기 (1) | 2024.11.27 |
| [프로그래머스-Lv1-JAVA] 달리기 경주 (0) | 2024.11.24 |

